これは Category Theory Advent Calendar 2018 16日目の記事です.
Twitter で「#豊穣圏は射が取れないからクソ」というハッシュタグの初出は(多分)これです.
豊穣圏PDFを紙に印刷して透かして見ると「#豊穣圏は射が取れないからクソ」と書いてあります
— alg_d (@alg_d) April 1, 2018
今回はこのハッシュタグの意味(?)について, 圏論ビギナー向け(?)の解説をします. 皆さんを射のない世界へとお連れしましょう.
(と言っても, alg_d 氏の「壱大整域」の豊穣圏 PDF を雑に端折った感じの内容です. なお各種図式はパクリではなくちゃんと一から自分で作っています.)
$\mathcal{B}$ がモノイダル圏であるとは $\mathcal{B}$ がただ一つの対象を持つ
bicategory であることを言います. ビギナー向け解説なのにいきなり bicategory の知識仮定しちゃうの?
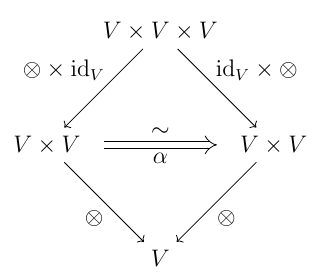
$\mathrm{Ob}(\mathcal{B}) = \{*\}$ として, $V := \mathcal{B}(*, *)$ と置いて諸々の条件を書き下してみましょう. まず二項演算として $\otimes := C_{***} \colon V \times V \to V$ と, いわゆる「単位元」となる $I := \mathrm{id}_* \in \mathrm{Ob}(V)$ があります. そのうえで, 以下のような自然同型があります.

コヒーレンス条件はこうなりますね.
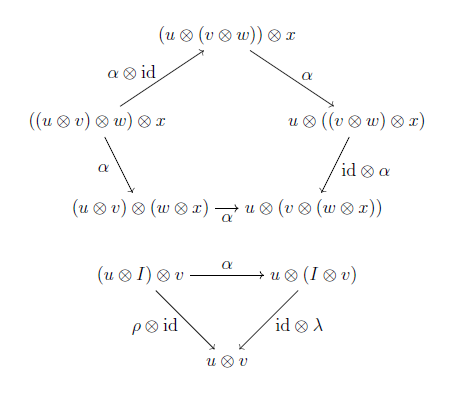
というわけで, 以下, 最初からこのような $V := \langle V, \otimes, I, \alpha, \lambda, \rho\rangle$ をモノイダル圏と言うことにしましょう.
ここから先の話はとりあえずなくても良いのですが, 仮定しておくといろいろと楽(?)なので載せておきます.
モノイダル圏 $V$ が対称であるとは, $u, v \in \mathrm{Ob}(V)$ について自然な同型 $\gamma_{uv} \colon u \otimes v \to v \otimes u$ があって, $\gamma_{vu} \circ \gamma_{uv} = \mathrm{id}_{u \otimes v}$ かつ, 以下の図式が可換になることを言います.
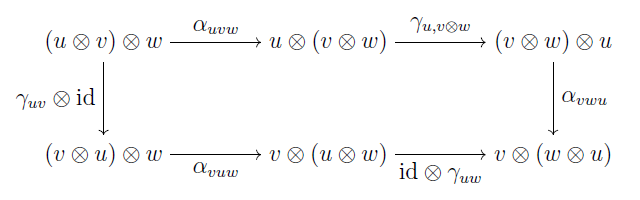
さらに, (対称)モノイダル圏 $V$ が閉であるとは, 任意の $u \in \mathrm{Ob}(V)$ に対して函手 $- \otimes u \colon V \to V$ が右随伴(これを $[u, -]$ で表す)を持つことを言います.
モノイダル閉圏 $V$ において $u, v, w \in \mathrm{Ob}(V)$ とするとき $$V(u \otimes v, w) \cong V(u, [v, w])$$ で, かつ $x$ について自然に $$\begin{align} V(x, [u \otimes v, w]) &\cong V(x \otimes (u \otimes v), w) \\ &\cong V((x \otimes u) \otimes v, w) \\ &\cong V(x \otimes u, [v, w]) \\ &\cong V(x, [u, [v, w]]) \end{align}$$ なので, 米田の補題から $[u \otimes v, w] \cong [u, [v, w]]$ が成り立ちます. また, $V$ が対称なら $$[u, [v, w]] \cong [u \otimes v, w] \cong [v \otimes u, w] \cong [v, [u, w]]$$ も成り立ちます.
随伴 $- \otimes u \dashv [u, -]$ の余単位(counit)を $\mathrm{ev} \colon [u, -] \otimes u \Rightarrow \mathrm{id}$ と書きます. また, この随伴で $\rho \colon u \otimes I \to u$ に対応する射を $i \colon u \to [I, u]$ と書きます. $i$ は同型射になります(証明略).
$\mathbf{Set}, \mathbf{Cat}, \mathbf{2} = \{0 \to 1\}$ は直積を積, 終対象を単位元として対称モノイダル閉圏になります. また, $\mathbf{Ab}$ は(加群の)テンソル積を積, 有理整数環 $\mathbb{Z}$ を単位元としてやはり対称モノイダル閉圏になります.
ちょっと変わったところで $\bar{\mathbb{R}}_+ := [0, \infty]$ を考えてみましょう. これに通常の大小関係と逆の順序を入れて圏とみなします.
これをモノイダル圏とみなすには, 実数の和を積とし, $0$ を単位元とします. $\bar{\mathbb{R}}_+$ は明らかに対称モノイダル圏になります.
$$[u, v] := \begin{cases} 0 & (v \le u) \\ \infty & (u \lt v = \infty) \\ v - u & (u \lt v \lt \infty) \end{cases}$$ と置けば, 対称モノイダル閉圏になることが示せます(そんなに難しくないです).
いよいよ問題(?)の豊穣圏を定義する準備ができました.
$V$ を(対称)モノイダル(閉)圏とするとき, $\mathcal{C}$ が $V$-豊穣圏(enriched category)であるとは, 以下を満たすことである.
次図が可換.
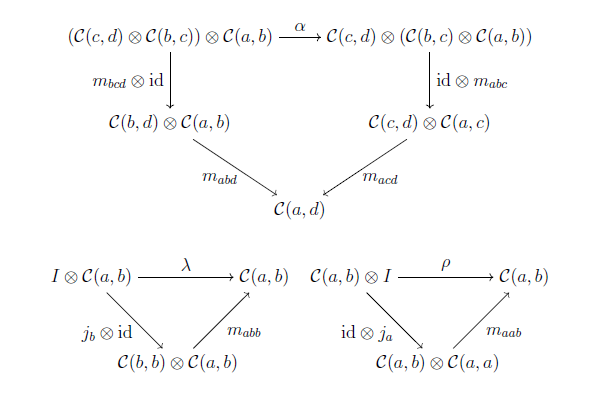
さて, 豊穣圏の定義は分かりました. $V$-豊穣圏 $\mathcal{C}$ では $\mathcal{C}(a, b)$ が「射の集まり」のような役割を果たすわけです. でもちょっと待って! $\mathcal{C}(a, b)$ ってあくまでも「モノイダル圏 $V$ の対象」でしかないんです. 集合になってる保障すらありません. ってことは...?
は?? 射が取れないんだが~??
どうやら「豊穣圏は射が取れない」のは本当のようです.
????「豊穣圏はわるい文明! さらば!」

いや待て落ち着け.
$V$-豊穣圏の $V$-函手が定義できます. $F \colon \mathcal{C} \to \mathcal{D}$ が $V$-函手であるとは
次図が可換.
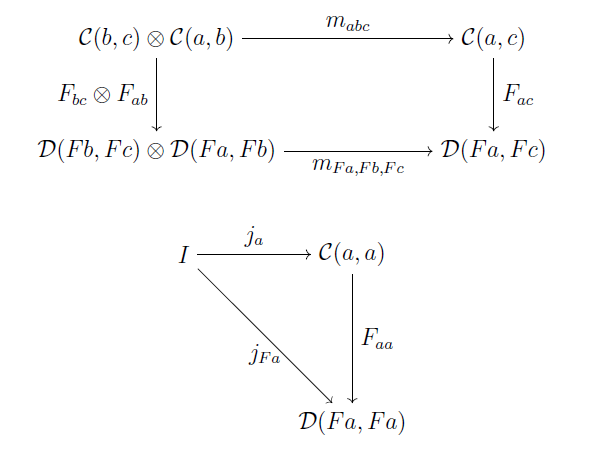
$V$-函手 $F \colon \mathcal{A} \to \mathcal{B}, G \colon \mathcal{B} \to \mathcal{C}$ に対して $G \circ F \colon \mathcal{A} \to \mathcal{C}$ を $$(G \circ F)a = G(Fa), (G \circ F)_{ab} = G_{Fa, Fb} \circ F_{ab} \colon \ \mathcal{A}(a, b) \to \mathcal{C}(GFa, GFb)$$ と定義すれば, 合成 $V$-函手が定義できます(可換性を確かめてみよう!). これにより, $V$-豊穣圏の全体 $V$-$\mathbf{Cat}$ は(普通の)圏になります. 良かった.
$V$-函手間の $V$-自然変換も定義できます. $F, G \colon \mathcal{C} \to \mathcal{D}$ が $V$-函手のとき, $V$-自然変換 $\theta \colon F \Rightarrow G$ とは $$\{ \theta_a \colon I \to \mathcal{D}(Fa, Ga)\}_{a \in \mathrm{Ob}(\mathcal{C})}$$ で次の図式が可換になるものを言います.
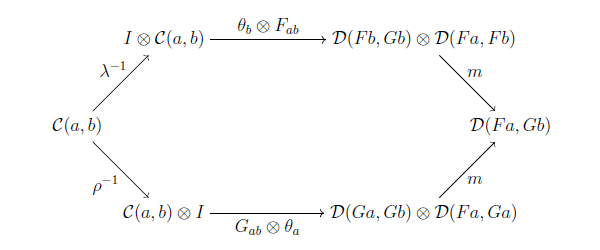
そしてなんと, $V$-$\mathbf{Cat}$ は $V$-豊穣圏を 0-cell, $V$-函手を 1-cell, $V$-自然変換を 2-cell として2-圏になります. 2-圏は良い文明です.
$\mathbf{Set}$-豊穣圏は局所小圏, $\mathbf{Set}$-函手は(局所小圏間の)普通の函手です. $\mathbf{Cat}$-豊穣圏は2-圏のことですね. $\mathbf{Cat}$-函手は (strict) 2-函手です.
(対称)モノイダル閉圏 $V$ は, 以下のようにしてそれ自身を $V$-豊穣圏 $\mathcal{V}$ とみなせます.
少し変わった例も見てみましょう. $(X, d)$ を距離空間とするとき, 以下のようにして $\bar{\mathbb{R}}_+$-豊穣圏 $\mathcal{C}$ を定めることができます.
つまり距離空間は $\bar{\mathbb{R}}_+$-豊穣圏とみなせます. 逆に $\bar{\mathbb{R}}_+$-豊穣圏は一般化された距離空間だと思えます. $\bar{\mathbb{R}}_+$-函手は Lipschitz 定数が $1$ 以下の Lipschitz 連続関数と思えます.
さて, 本当に「#豊穣圏は射が取れないからクソ」なんでしょうか.
$V$-$\mathbf{Cat}$ は2-圏になるという話をしました. 大事なことなのでもう一度言いますが, 2-圏は良い文明です. みんな大好き Kan 拡張チャンス!
普通の圏だと射が取れるから対角函手が自然に定義できて (co)limit が対角函手の随伴として定義できますが, 豊穣圏だと射が取れないからそもそも対角函手が自然に定義できません. でも「通常の圏で (co)limit を各点 Kan 拡張だと思うとどうなるか」から逆算をして, 各点 Kan 拡張ができるように (co)limit の類似物を定義することが出来そうです. 実際できます.
ざっくりと定義だけ書いておきますと, $\mathcal{C}, \mathcal{J}$ が $V$-豊穣圏で, $F \colon \mathcal{J} \to \mathcal{C}, W \colon \mathcal{J} \to \mathcal{V}$ を $V$-函手とします. $V$-函手 $$c \mapsto [\mathcal{J}, \mathcal{V}](W-, \mathcal{C}(c, F-))$$ が表現可能なとき, その表現対象を weighted limit と言い, ${\lim}^W F$ と書きます. つまり $$\mathcal{C}(c, {\lim}^W F) \cong [\mathcal{J}, \mathcal{V}](W-, \mathcal{C}(c, F-))$$ というわけです. $V = \mathbf{Set}, W = \Delta 1$ (定数函手)とすれば ${\lim}^{\Delta 1} F \cong \lim F$ になるなので, なるほどこれはちゃんと limit の類似品になっているようです. そう言えば某どころの本ではこの weighted limit が紹介されているそうですが, 専門家の先生が書かれた本ですからきっとボクより上手に説明してるんだろうなぁ(しろめ).
こうして(通常の)圏論において「全ての概念は Kan 拡張である」ことを利用して,
豊穣圏での類似の概念が得られました. やはり全ての概念は Kan 拡張である.
大事なことなので2回言いました.
そんなわけで豊穣圏でも普通の圏論とほぼ同様の理論が展開できます. ただ随分面倒くさいです. alg_d 氏が PDF にまとめるのも大変な作業だったと思います(特に Tikz で図式描くのとか). その気持ちを氏がハッシュタグに込めたのが「#豊穣圏は射が取れないからクソ」だったのでしょう.
良かった, 豊穣圏でも大丈夫だ. 問題ない. 理解できたとは言ってない
半月前に「対象なんてただの飾りです」という話をしたわけですが, 豊穣圏はさらに踏み込んで「射なんてただの飾りです」といったところでしょうか.
このあたりのことはちゃんと説明しようとするとものすごいボリュームになるので豪快に端折って書いてますっていうか, その辺は下手な私の解説より「壱大整域」の方が詳しいですが,
ふいんき(何故か変換できない)くらいは伝わったでしょうか.
全ての categorist に Kan 拡張のあらんことを.
赤猫堂本舗「数学に関するよしなしごと」へ