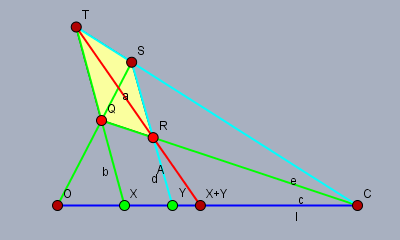
$\{c, x, o, c, y, z\}$ が四角形性六点であるとき $z := x + y$ とする.
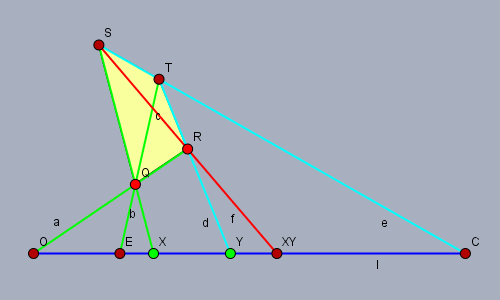
$\{o, x, e, c, y, z\}$ が四角形性六点であるとき $z := xy$ とする.
射影空間内の直線 $l$ 上の順序付けられた異なる三点 $\{o, c, e\}$ を標構と言い, $o$ を原点, $c$ を示点, $e$ を単位点と言う.
直線 $l$ 上に標構 $\{o, c, e\}$ が与えられたとき, $l$ 上の $c$ と異なる点 $x, y$ に対して以下のように和と積を定義する.
$\{c, x, o, c, y, z\}$ が四角形性六点であるとき $z := x + y$ とする.

$\{o, x, e, c, y, z\}$ が四角形性六点であるとき $z := xy$ とする.

各々が体の和・積としての性質を満たすことは別頁にて示す. この和と積によって $l$ 上の $c$ を除く点の全体がなす体を $K(o, c, e)$ で表し, Staudt 代数(あるいは直線体)という.