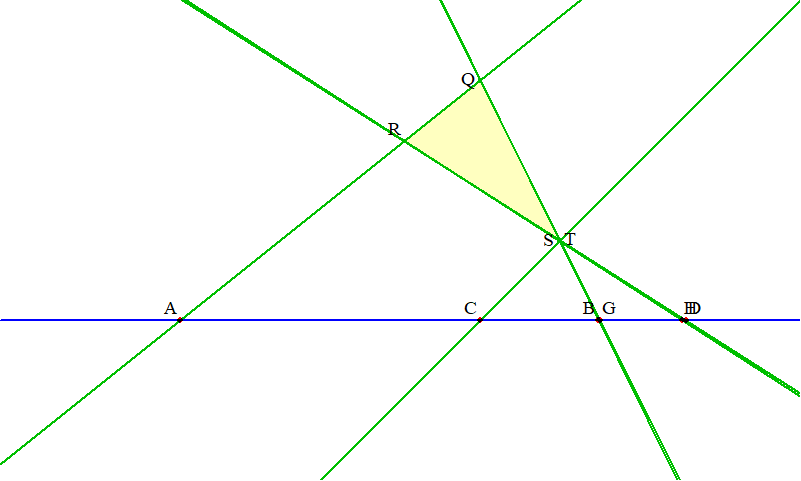
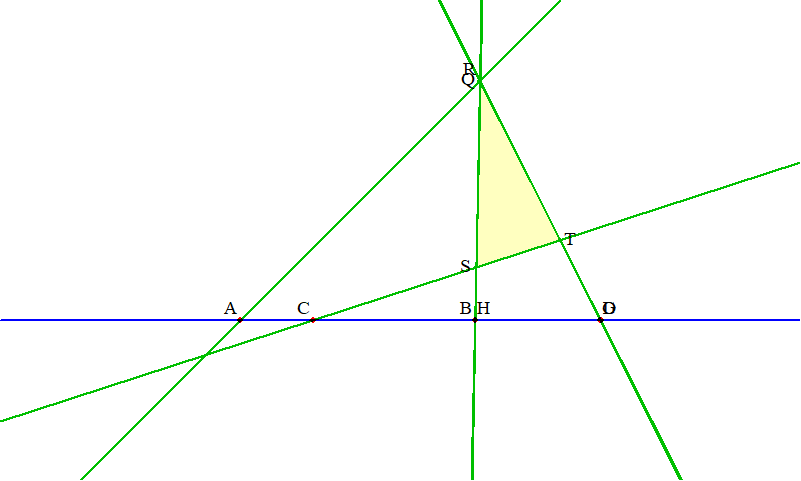
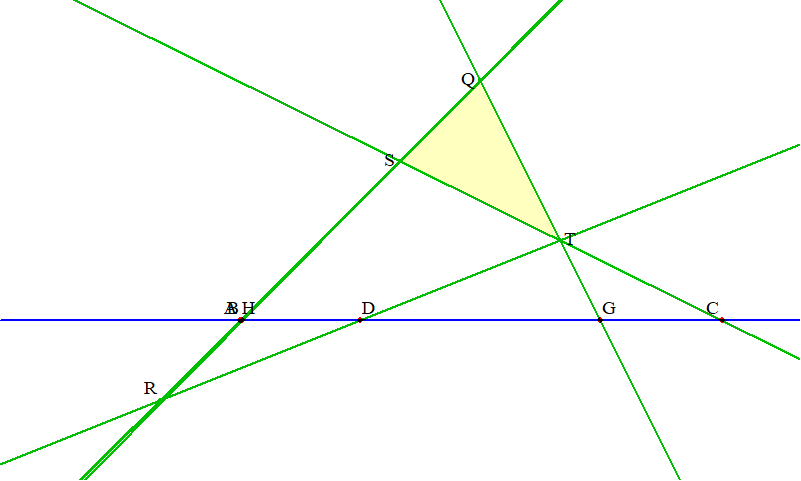
同一平面上にあって, どの三点も共線でないような四点 $a_1, a_2, a_3, a_4$ があるとき, これらの点および六直線 $a_i\vee a_j\ (i, j = 1, 2, 3, 4, i\ne j)$ を合わせて(完全)四角形という. $$\square(a_1, a_2, a_3, a_4) = \{a_i, a_j\vee a_k | i = 1, 2, 3, 4, j, k = 1, 2, 3, 4, j\ne k\}.$$ 点を頂点, 直線を辺という. また同じ頂点を通らない二辺は互いに他の対辺という.
双対的に(完全)四辺形も定義される.
二つの四角形 $\square(a_1, a_2, a_3, a_4), \square(b_1, b_2, b_3, b_4)$ について, $a_i\vee a_j, b_i\vee b_j\ (i, j = 1, 2, 3, 4, i\ne j)$ のうち五組が交わり, かつ交点が共線であるとするならば, 残りの一組も交わり, かつ交点は他の五交点と共線である.
$a_3\vee a_4, b_3\vee b_4$ 以外の五組が交わり, かつ交点が共線であると仮定してよい.
このとき $\mathit{\Delta}(a_1, a_2, a_3)$ と $\mathit{\Delta}(b_1, b_2, b_3)$, $\mathit{\Delta}(a_1, a_2, a_4)$ と $\mathit{\Delta}(b_1, b_2, b_4)$ のそれぞれに Desargues の定理の逆を適用すれば $a_1\vee b_1, a_2\vee b_2, a_3\vee b_3, a_4\vee b_4$ は共点である.
故に $\mathit{\Delta}(a_1, a_3, a_4)$ と $\mathit{\Delta}(b_1, b_3, b_4)$ に Desargues の定理を適用すれば $a_3\vee a_4$ と $b_3\vee b_4$ も交わり, かつ交点は他の五点と共線である.
(証明終)
同一直線 $l$ 上の六点 $\{p, q, r, s, t, u\}$ は, 四角形 $\square(a_1, a_2, a_3, a_4)$ が存在して, 各々がその辺のいずれかと $l$ との交点であるとき, 四角形性を持つという. ただし
- $p, q, r$ を通る辺は四角形のある頂点が共点
- $p$ と $s$, $q$ と $t$, $r$ と $u$ は互いに対辺の上にある
とする.
定理 5 により, 六点の四角形性は四角形の取り方によらない.
注意 : 定義からわかる通り四角形性六点は点の順序が重要である. 任意に順序を入れ替えたものが四角形性を持つとは限らない. ただし $\{p, q, r, s, t, u\}$ が四角形性を持てば $\{q, r, p, t, u, s\}, \{s, t, r, p, q, u\}$ 等は四角形性を持つ.
双対的に六直線 $\{l, m, n, g, h, k\}$ の四辺形性も定義される.
$o$ を共点とする四辺形性六直線 $\{l, m, n, g, h, k\}$ と $o$ を通らない直線 $s$ との交点を $\{p, q, r, a, b, c\}$ とすれば $\{a, b, c, p, q, r\}$ は四角形性六点である.
四辺形性を与える四辺形の一頂直線として $s$ を選んでよい. 他の三頂直線 $t, u, v$ としてそれぞれ $p, q, r$ を通るものを取り $$x_1 := u\cap v, x_2 := v\cap t, x_3 := t\cap u$$ とすれば $\square(o, x_1, x_2, x_3)$ が $\{a, b, c, p, q, r\}$ の四角形性を与える.
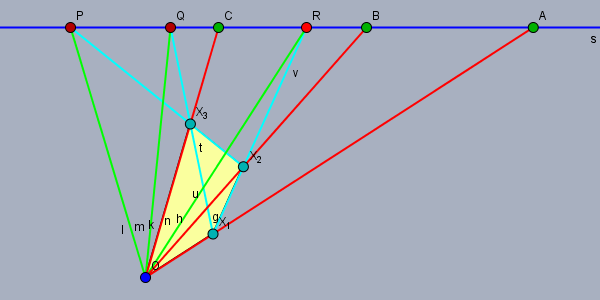
(証明終)
六点の四角形性は射影変換によって保たれる.
定理 6 およびその双対から明らかである.