配景写像と射影変換

配景写像

定義 2

$n$ 次元射影空間の二つの $r (\lt n)$ 次元面 $\alpha, \beta$ に対し, 配景の軸 $c$ を取る.

$x\in\alpha$ に対して $$\pi_{\beta\alpha}(c)(x) := (x\vee c)\cap\beta$$ とおくと $\pi_{\beta\alpha}(c) : \alpha \to \beta$ が定まる. これを $c$ を軸とする配景写像という.

命題(配景写像の基本性質)

配景写像に関して以下の性質が成り立つ.

$x\in\alpha\cap\beta$ ならば $\pi_{\beta\alpha}(c)(x) = x.$
$\pi_{\beta\alpha}(c)^{-1} = \pi_{\alpha\beta}(c).$
$\gamma$ を $c$ の補元とするとき $\pi_{\beta\alpha}(c) = \pi_{\beta\gamma}(c)\circ\pi_{\gamma\alpha}(c).$
$\pi_{\beta\alpha}(c) = \pi_{\beta\alpha}(c\cap s).$ ただし右辺は空間 $s = \alpha\vee\beta$ 内の配景写像.

証明

いずれもモジュラー律を用いて容易に示すことができる.

射影変換

定義 3

$l, g$ を射影空間内の直線とする. $\varphi : l\to g$ が射影変換であるとは, $\varphi$ が有限個の配景写像の合成であることを言う.

注意 : この定義は $n$ 次元射影空間の $r (\lt n)$ 次元面に対して自然に拡張することができるが, 空間自身には適用できない.

定理 3

二直線 $l, g$ 上にそれぞれ相異なる三点 $\{a, b, c\}, \{a', b', c'\}$ をとるとき, $$\varphi(a) = a', \varphi(b) = b', \varphi(c) = c'$$ となる射影変換 $\varphi : l\to g$ が存在する.

証明

[1] $l\ne g, \emptyset\ne l\cap g = a = a'$ の場合

$\mathit{\Delta}(a, b, b')$ に PG2 を用いれば, 二直線 $b\vee b', c\vee c'$ は一点 $s$ で交わる. 故に $\varphi = \pi_{gl}(s)$ と置けばよい.

$b = b'$ あるいは $c = c'$ の場合も同様.

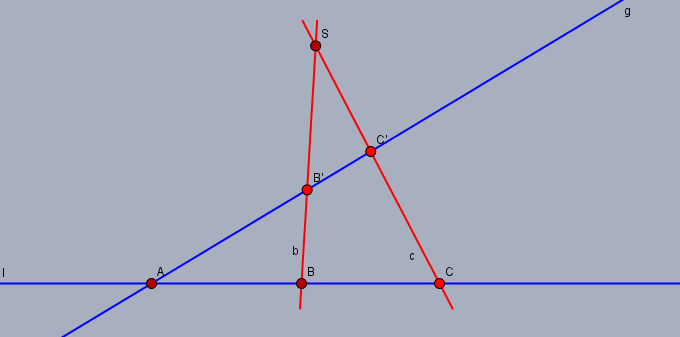
[2] $l\ne g, a\ne a', b\ne b', c\ne c'$ の場合

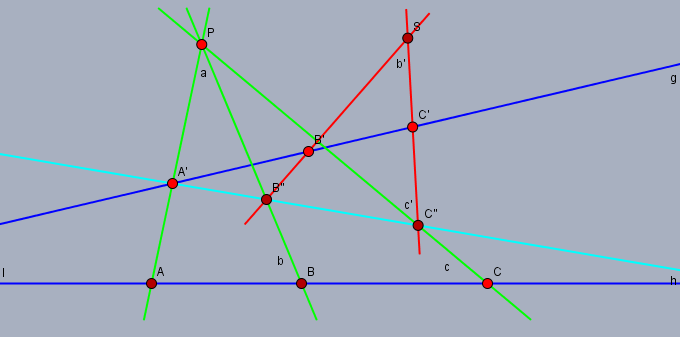
$l\cap g\ne a'$ と仮定してよい. 直線 $a\vee a'$ 上の点 $p(\ne a, a')$ を取り, $a'$ を通り平面 $l\vee(a\vee a')$ に含まれる直線 $h(\ne g, a\vee a')$ を取る.

$\pi_{hl}(p)$ と二直線 $h, g$ に対する [1] によって作られる変換とを結合すれば求める変換が得られる.

[3] $l = g$ の場合

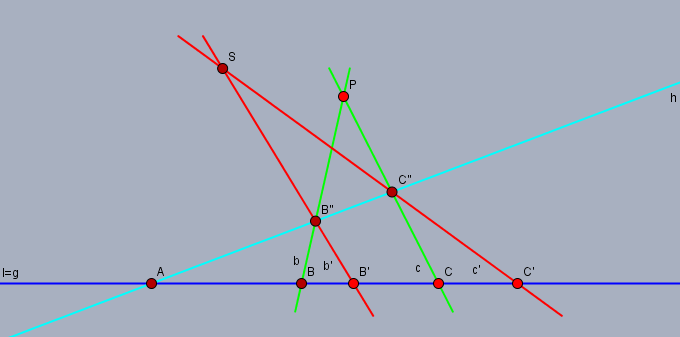
$l$ 上にない点 $p$ および平面 $p\vee l$ に含まれる直線 $h(\ne l, p\not\in h)$ を取って $\pi_{hl}(p)$ を取れば [1] または [2] に帰着される.

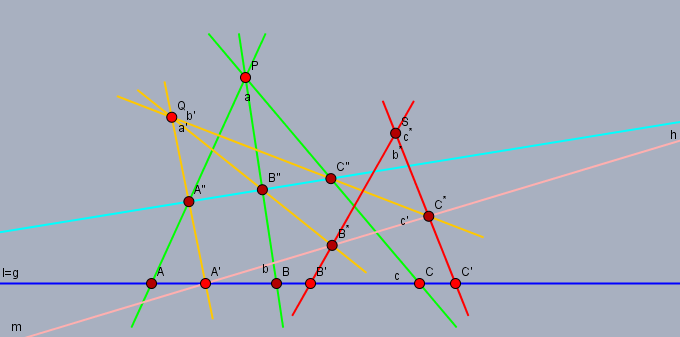
(証明終)

定理 4

射影変換 $\varphi : l\to g$ は部分空間における点を軸とする配景写像の結合として表される.

証明

配景写像 $\pi_{gl}(c)\ (\mathrm{dim}(c) = n - 2)$ の場合に示せば十分である. $l = g$ ならば $\pi_{gl}(c)$ は恒等変換ゆえ自明. $l\ne g, l\cap g\ne\emptyset$ のとき $$\begin{align} \mathrm{dim}(l\vee g) &= \mathrm{dim}(l) + \mathrm{dim}(g) - \mathrm{dim}(l\cap g) \\ &= 1 + 1 - 0 \\ &= 2 \end{align}$$ ゆえ $l\vee g$ は平面. よって $$\begin{align} \mathrm{dim}(c\cap(l\vee g)) &= \mathrm{dim}(c) + \mathrm{dim}(l\vee g) - \mathrm{dim}(c\vee(l\vee g)) \\ &= \mathrm{dim}(c) + \mathrm{dim}(l\vee g) - \mathrm{dim}((c\vee l)\vee g) \\ &= \mathrm{dim}(c) + \mathrm{dim}(l\vee g) - \mathrm{dim}(P_n\vee g) \\ &= \mathrm{dim}(c) + \mathrm{dim}(l\vee g) - \mathrm{dim}(P_n) \\ &= (n - 2) + 2 - n \\ &= 0 \end{align}$$ となり $p:= c\cap(l\vee g)$ は点である.

$l\cap g = \emptyset$ のときは $$\begin{align} \mathrm{dim}(l\vee g) &= \mathrm{dim}(l) + \mathrm{dim}(g) - \mathrm{dim}(l\cap g) \\ &= 1 + 1 - (- 1) \\ &= 3, \end{align}$$ $$\begin{align} \mathrm{dim}(c\cap(l\vee g)) &= \mathrm{dim}(c) + \mathrm{dim}(l\vee g) - \mathrm{dim}(P_n) \\ &= (n - 2) + 3 - n \\ &= 1 \end{align}$$ ゆえ $k:= c\cap(l\vee g)$ は直線である.

$x\in l, y\in g$ を $y\ne\pi_{gl}(k)(x)$ となるように取れば $h:= x\vee y$ は $k$ と交わらぬゆえ $$\begin{align} \pi_{gl}(c) &= \pi_{gl}(k) \\ &= \pi_{gh}(k)\circ\pi_{hl}(k) \\ &= \pi_{gh}(q)\circ\pi_{hl}(p). \end{align}$$ ここに $p:= k\cap(l\vee h), q:= k\cap(h\vee g)$ は点である.

(証明終)

戻る