Pappus 性と係数体の可換性

Pappus 性

定義 8

射影空間において Pappus 性が成り立つとは, 同一平面上の異なる二直線 $l, l'$ のそれぞれの上の異なる三点 $\{a, b, c\}, \{a', b', c'\}$ について三交点 $$(b\vee c')\cap(b'\vee c), (c\vee a')\cap(c'\vee a), (a\vee b')\cap(a'\vee b)$$ が共線であることをいう.

射影変換の単一性

異なる二直線 $l, l'$ のそれぞれの上の異なる三点 $\{a, b, c\}, \{a', b', c'\}$ の対応 $$a\to a', b\to b', c\to c'$$ が与えられると, 射影変換 $\varphi : l\to l'$ で $$\varphi(a) = a', \varphi(b) = b', \varphi(c) = c'$$ を満たすものが存在するが, $\varphi$ がそのようなただ一つの射影変換であるというのが射影変換の単一性である.

射影変換の単一性は次のように言い換えられる.

(*)「同一直線上の異なる三点を動かさない射影変換は恒等変換に限る.」

実際, 射影変換の単一性を仮定して, $l$ 上の射影変換 $\theta : l\to l$ が異なる三点 $\{a, b, c\}$ を動かさない, すなわち $$\theta(a) = a, \theta(b) = b, \theta(c) = c$$ とする. $l'(\ne l)$ 上の異なる三点 $\{a', b', c'\}$ に対し, 射影変換 $\varphi : l\to l'$ で $$\varphi(a) = a', \varphi(b) = b', \varphi(c) = c'$$ となるものを取ると, 明らかに $$\varphi\circ\theta(a) = \varphi(a) = a', \varphi\circ\theta(b) = \varphi(b) = b', \varphi\circ\theta(c) = \varphi(c) = c'$$ が成り立つので, 射影変換の単一性により $\varphi\circ\theta = \varphi$. 左から $\varphi^{-1}$ を作用させて $\theta = \mathrm{id}_l$ となる.

逆に (*) が成り立つと仮定すると, 異なる二直線 $l, l'$ のそれぞれの上の異なる三点 $\{a, b, c\}, \{a', b', c'\}$ と射影変換 $\varphi, \psi : l\to l'$ について $$\varphi(a) = \psi(a) = a', \varphi(b) = \psi(b) = b', \varphi(c) = \psi(c) = c'$$ が成り立てば $$\psi^{-1}\circ\varphi(a) = a, \psi^{-1}\circ\varphi(b) = b, \psi^{-1}\circ\varphi(c) = c$$ が成り立つから $\psi^{-1}\circ\varphi = \mathrm{id}_l$. 左から $\psi$ を作用させて $\varphi = \psi$ となる.

両者をまとめて射影変換の単一性ということにする. さらに以下が成り立つ.

定理 11

射影変換の単一性は以下と同値である. 「交わる二直線 $l, g(\ne l)$ の交点を動かさない射影変換 $\varphi : l\to g$ は, 平面 $l\vee g$ 内のある点 $p$ を軸とする配景写像 $\pi_{gl}(p)$ に一致する.」

証明

$l$ 上に $a = l\cap g$ とは異なる二点 $b, c(\ne b)$ を取り, $b' := \varphi(b), c' := \varphi(c)$ と置く. $p := (b\vee b')\cap(c\vee c')$ と置けば $\varphi$ と $\pi_{gl}(p)$ はともに $$a\to a, b\to b', c\to c'$$ なる射影変換であるから両者は一致する.

逆に $\theta : l\to l$ が異なる三点 $a, b, c$ を動かさないものとする. $a$ を通り $l$ とは異なる直線 $g$ を取り, $l, g$ の(平面 $l\vee g$ 内における)背景の軸 $p$ を取って配景写像 $\psi := \pi_{gl}(p)$ を考え, $b' := \psi(b), c' := \psi(c)$ と置く. このとき射影変換 $\psi\circ\theta : l\to g$ について $$\psi\circ\theta(a) = \psi(a) = a, \psi\circ\theta(b) = \psi(b) = b', \psi\circ\theta(c) = \psi(c)= c'$$ であるから, $\psi\circ\theta$ は $(b\vee b')\cap(c\vee c') = p$ を背景の軸とする配景写像, すなわち $\psi\circ\theta = \psi$ となるので $\theta = \mathrm{id}_l$ となり射影変換の単一性が成り立つ.

(証明終)

定理 12

射影空間に対して以下の三条件は同値である.

1. 係数体が可換である.
2. 射影変換の単一性が成り立つ.
3. Pappus 性が成り立つ.

証明

1. ⇒ 2.

係数体が可換ならば内部自己同型は恒等変換に限るので, これは Staudt 代数の標構を動かさない射影変換が恒等写像である, すなわち射影変換の単一性を意味する

2. ⇒ 3.

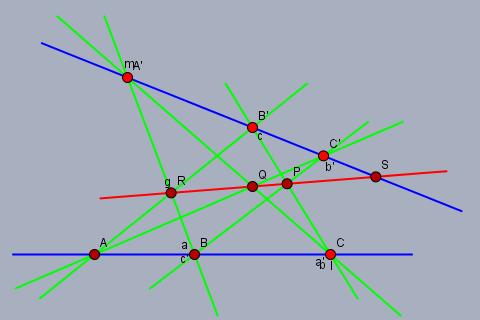
同一平面上の二直線 $l, l'$ の標構 $\{a, b, c\}, \{a', b', c'\}$ に対して $$p := (b\vee c')\cap(b'\vee c), q := (c\vee a')\cap(c'\vee a), r := (a\vee b')\cap(a'\vee b)$$ と置く. 直線 $g := q\vee r$ と直線 $l', b\vee c', b'\vee c$ との交点をそれぞれ $s, x_1, x_2$ とする. 射影変換 $\varphi : g\to g$ を $$\varphi := \pi_{g, a'\vee c}(b')\circ\pi_{a'\vee c, a'\vee b}(a)\circ\pi_{a'\vee b, g}(c')$$ と置くと $$\varphi(q) = q, \varphi(r) = r, \varphi(s) = s, \varphi(x_1) = x_2$$ 故, 射影変換の単一性により $x_1 = x_2$ であり, 明らかにそれは $p$ に一致するから $p\in g$ である. つまり $p, q, r$ は共線である.

3. ⇒ 1.

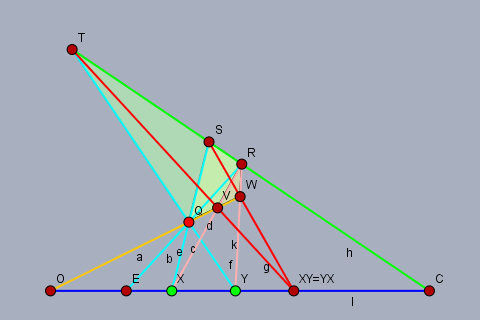
直線 $l$ 上の標構 $\{o, c, e\}$ と $l$ 上の $o, c, e$ とは異なる二点 $x, y$ が与えられているとする. $c$ を通る直線 $h(\ne l)$ と, 平面 $l\vee h$ 上の点 $q(\not\in l, h)$ を取り $$r := h\cap(q\vee e), s := h\cap(q\vee x), t := h\cap(q\vee y)$$ とする. また $$v := (o\vee q)\cap(r\vee x), w := (o\vee q)\cap(r\vee y)$$ とし, $z := (s\vee w)\cap(t\vee v)$ とおくと Pappus 性により $x, y, z$ は共線となる. すなわち $z\in l$ である. このとき $\square(q, w, r, s)$ が $\{o, x, e, c, y, z\}$ の四角形性を与え, $\square(q, v, r, t)$ が $\{o, y, e, c, x, z\}$ の四角形性を与えるから, $xy = z = yx$ である. $xo = ox = o, xe = ex = x$ であるから, $x, y$ のいずれか一方が $o$ または $e$ に一致するときは明らかに $xy = yx$ が成り立つ.

戻る