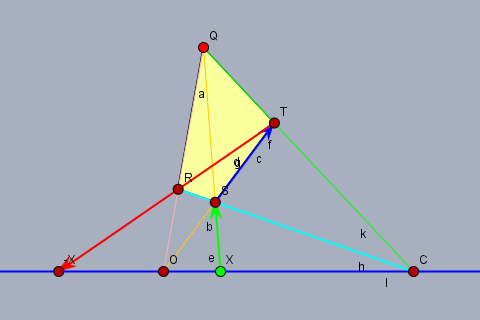
和の定義図よりただちに $\{c, y, o, c, x, x + y\}$ も四角形性六点であることがわかるから $y + x = x + y$ である.

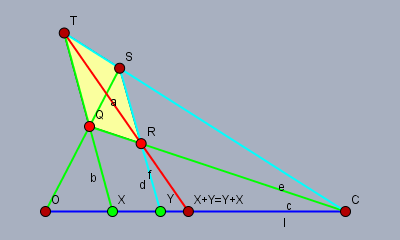
$\{c, x, o, c, y, x + y\}$ の四角形性を与える四角形 $\square(q, r, s, t)$ を取る. $m := (o\vee r)\cap(s\vee t), l := (z\vee m)\cap(q\vee r)$ とするとき, $\square(r, l, m, s)$ は $\{c, y, o, c, z, y + z\}$ の四角形性を与える.
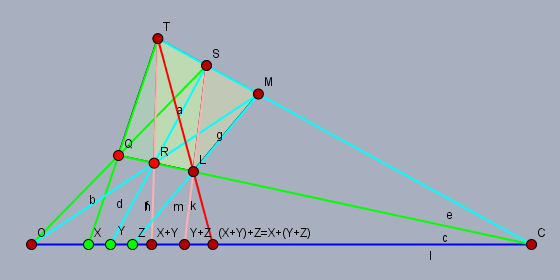
$w := (o\vee c)\cap(t\vee l)$ とおくと $\square(q, l, s, t)$ が $\{c, x, o, c, y + z, w\}$ の, $\square(r, l, m, t)$ が $\{c, x + y, o, c, z, w\}$ の四角形性をそれぞれ与えるから $$(x + y) + z = w = x + (y + z).$$
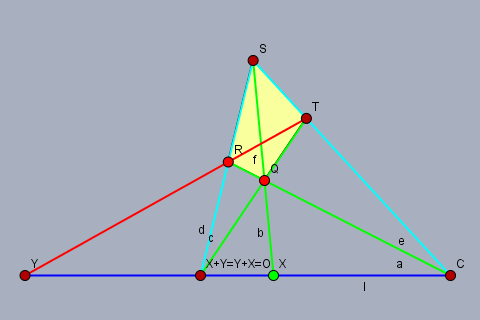
特殊ケース [2] により $\{c, x, o, c, o, x\}$ は四角形性六点である. また, 特殊ケース [1] により $\{c, o, o, c, x, x\}$ も四角形性六点である. よって $x + o = o + x = x.$
$o\vee c$ 上にない点 $q$ を任意に取り, $c\vee q$ 上に $c, q$ と異なる点 $r$ を取る.
$r := (o\vee r)\cap(x\vee q), t := (o\vee q)\cap(c\vee s), y := (o\vee c)\cap(r\vee t)$ と置けば $\square(q, r, s, t)$ は $\{c, x, o, c, y, o\}$ の四角形性を与えるから $x + y = y + x = o.$
直線 $l$ 上の原点, 示点をそれぞれ $o, c$ とする. $l$ 上にない任意の点 $q$, および平面 $l\vee q$ 内の直線 $h(\ne l, c\vee q)$ を取る. このとき, 適当な点 $r$ を取れば, 次のような射影変換 $\varphi : l\to l$ を作ることができる.
任意の点 $k\in l\ (k\ne c)$ を取る. $q, r, c$ は共線とし, $$\varphi := \pi_{lh}(r)\circ\pi_{hl}(q), \varphi(o) = k$$ とすれば $\varphi(x) = x + k\ (x\in l, x\ne c), \varphi(c) = (c).$
直線 $k := c\vee q$ を取る. $q, r, o$ は共線で, $r$ は $h$ 上にあるとし, $$\varphi := \pi_{lk}(r)\circ\pi_{kh}(o)\circ\pi_{hl}(q)$$ とすれば $\varphi(x) = - x\ (x\in l, x\ne c), \varphi(c) = c.$
和の定義を射影変換の言葉で言い換えたに過ぎない. $$s := (o\vee q)\cap h, r := (c\vee q)\cap(s\vee k), t := (x\vee q)\cap h$$ とすれば $\square(q, r, s, t)$ は四角形性六点 $\{c, x, o, c, k, \varphi(x)\}$ を定める. よって $\varphi(x) = x + k$ である. また明らかに $\varphi(c) = c$ である.
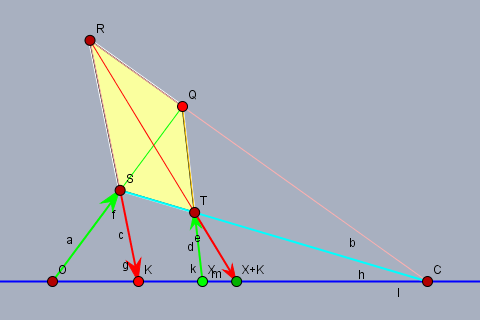
和の逆元を射影変換の言葉で言い換えたに過ぎない. $r := (o\vee q)\cap h$ とすればよい. $$s := (q\vee x)\cap h, t := (o\vee s)\cap k$$ とすれば $\square(q, r, s, t)$ は四角形性六点 $\{c, x, o, c, \varphi(x), o\}$ を定める. よって $\varphi(x) = - x$ である. また明らかに $\varphi(c) = c$ である.