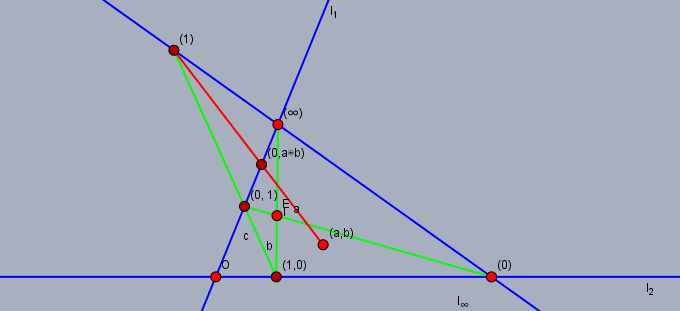
射影平面の点と直線に, 少なくとも二つの元 $0, 1(\ne 0)$ を含む集合 $R$ によって座標が与えられているものとする.
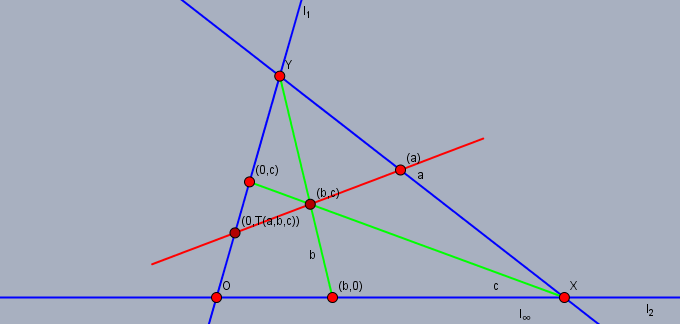
今, $R$ 上の三項演算 $T:R^3\to R$ を以下のように定義する. $a, b, c\in R$ に対して $(b, c)\in [a, k]$ であるとき $T(a, b, c) := k.$

このとき任意の $a, b, c\in R$ に対して $T(a, 0, c) = T(0, b, c) = c$ が成り立つ.
また, 任意の $a\in R$ に対して $T(a, 1, 0) = T(1, a, 0) = a$ が成り立つ.
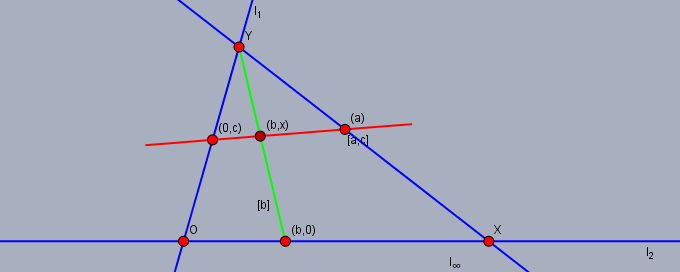
方程式 $$T(a, b, x) = c$$ がただ一つの解 $x\in R$ を持つことは $[a, c]$ と $[b]$ がただ一つの点で交わることと同義である.
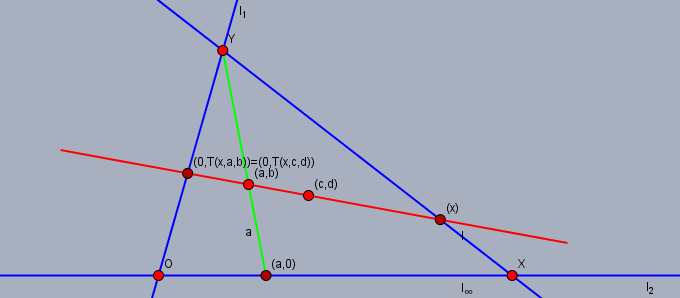
$a\ne c$ のとき, 方程式 $$T(x, a, b) = T(x, c, d)$$ がただ一つの解 $x\in R$ を持つことは, 二点 $(a, b), (c, d)$ を通る直線が $[x, y]$ に限る(ただし $y = T(x, a, b) = T(x, c, d)$)ことと同義である.
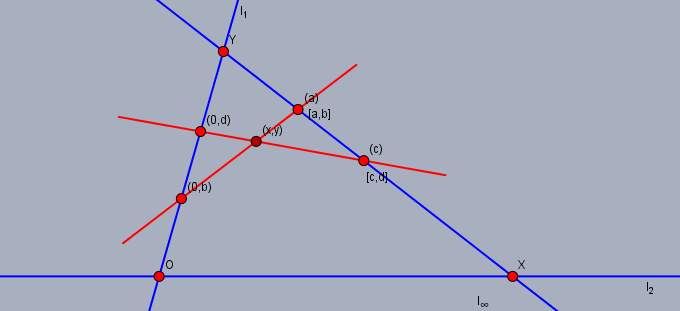
$a\ne c$ なる限りにおいて, 相異なる二直線 $[a, b], [c, d]$ は $[\infty]$ 上にないただ一つの点で交わる. これは方程式 $$T(a, x, y) = b, T(c, x, y) = d$$ がただ一つの解 $(x, y)\in R^2$ を持つことと同義である.
従って, 上のように定義した三項演算 $T$ によって $(R, T)$ は(平面)三項環となる.
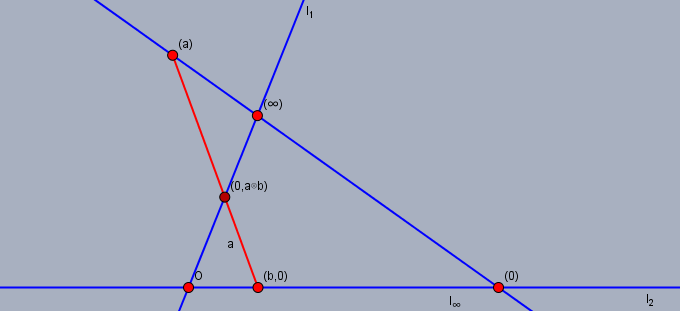
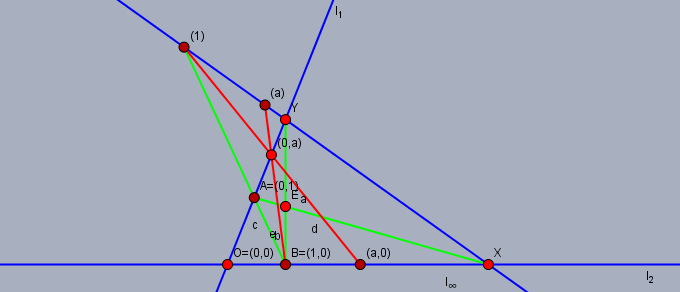
加法 $a\oplus b = T(1, a, b)$ と乗法 $a\otimes b = T(a, b, 0)$ を図示すると以下のようになる.