モジュラー束と特徴づけ

定義

一般の束において

• (M₁') $x\cup(y\cap (x\cup z))\le(x\cup y)\cap(x\cup z)$
• (M₂') $(x\cap y)\cup(x\cap z)\le x\cap(y\cup (x\cap z))$
• (M₃') $x\le z\Longrightarrow x\cup(y\cap z)\le(x\cup y)\cap z$

は常に成り立っていることは既に見たが

• (M₁) $x\cup(y\cap (x\cup z)) = (x\cup y)\cap(x\cup z)$
• (M₂) $(x\cap y)\cup(x\cap z) = x\cap(y\cup (x\cap z))$
• (M₃) $x\le z\Longrightarrow x\cup(y\cap z) = (x\cup y)\cap z$

のうちのどれか一つでも成り立っていれば全て成り立つ. 実際 $x\le z$ なる任意の $z$ は $z = x\cup z'$ と置けることから M₁ と M₃ は同等である. 双対的に M₂ と M₃ も同等であるから, 結局全て同等である.

束 $\mathcal{L}$ が M₁, M₂, M₃ のうちいずれか一つ(従って全て)を満たすとき, $\mathcal{L}$ はモジュラー束であると言う.

M₁ と M₂ は互いに双対, M₃ は自己双対であるから, $\mathcal{L}$ がモジュラー束ならばその双対束 $\mathcal{L}^*$ もモジュラー束である. 故にモジュラー束において成り立つ関係式についてはその双対が成り立つ.

特徴づけ

定理1

束 $\mathcal{L}$ がモジュラー束であるための必要十分条件は, 以下の Hasse 図で表現される部分束が存在しないことである.

(証明)

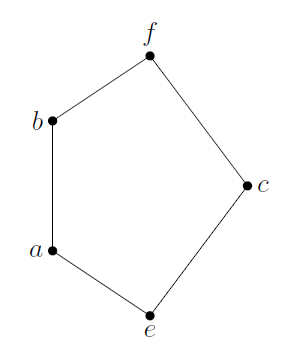
図のような部分束が存在すれば, $a\lt b$ ¹であるにも関わらず $$a\cup (c\cap b) = a\cup e = a\lt b = f\cap b = (a\cup c)\cap b$$ だから $\mathcal{L}$ はモジュラー束ではない.

逆に $\mathcal{L}$ がモジュラー束でなければ $$x\lt z, x\cup (y\cap z)\lt (x\cup y)\cap z$$ となる $x, y, z$ が存在する. そこで $$e = y\cap z, f = x\cup y, a = x\cup e, b = z\cap f$$ と置くと $$e\le a\lt b\le f, e\le y\le f$$ であるから $$e\le a\cap y\le b\cap y = f\cap z\cap y = f\cap e = e,$$ 従って $$a\cap y = b\cap y = e.$$ 双対的に $$f\ge b\cup y\ge a\cup y = e\cup x\cup y = e\cup f = f$$ なので $$a\cup y = b\cup y = f.$$

このとき $y$ は $a, b$ と比較不能である. 仮に $y\le a$ ならば $a = a\cup y = f$ となり矛盾. $a\le y$ としても $e = a, f = y$ となるので $b\le y$ となり $b = e$ が導かれるので矛盾する. 双対的に $b$ も $y$ と比較不能である.

以上を Hasse 図にすると下図のようになるので十分性も示された.

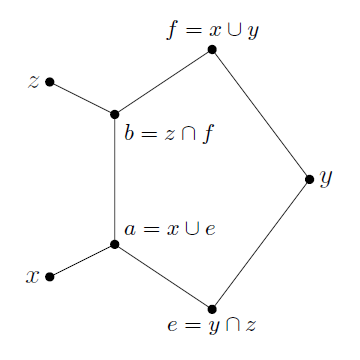
(証明終)

1. $a\le b$ かつ $a\ne b$ を一般に $a\lt b$ と表す.

戻る