5-lemma の証明 ～明日使える飲み会の余興～

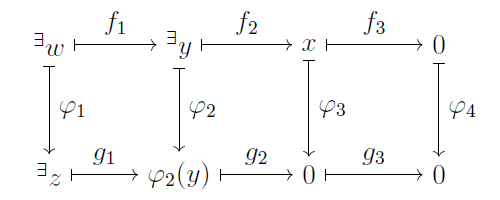
これは Math Advent Calendar 2018 24日目の記事です.

初めに

「東大数学科の飲み会では余興で 5-lemma の証明をやります」って某K澄の御大から聞いたんですけど本当なんでしょうか?ともあれ, あなたもこれを読めば飲み会で 5-lemma の証明ができるようになるはず!

5-lemma とは

ステートメント

次図は可換な加群の図式で, 各行は完全系列であるとします. $$\begin{CD} M_1 @>{f_1}>> M_2 @>{f_2}>> M_3 @>{f_3}>> M_4 @>{f_4}>> M_5 \\ @VV{\varphi_1}V @VV{\varphi_2}V @VV{\varphi_3}V @VV{\varphi_4}V @VV{\varphi_5}V \\ N_1 @>{g_1}>> N_2 @>{g_2}>> N_3 @>{g_3}>> N_4 @>{g_4}>> N_5. \end{CD}$$ このとき以下が成り立つというのが 5-lemma です.

  1. $\varphi_1$ が全射で $\varphi_2, \varphi_4$ が単射ならば $\varphi_3$ も単射.
  2. $\varphi_5$ が単射で $\varphi_2, \varphi_4$ が全射ならば $\varphi_3$ も全射.

さあ, 証明だ!

証明するとき, さらさらと図を描きながらやると盛り上がります(多分). なのでなるべく図付きで解説します.

まず 1. から証明しましょう. $\varphi_3(x) = 0 \Rightarrow x = 0$ を証明すればいいわけですよね. 実際 $\varphi_3(x) = 0$ と仮定すると $$\begin{align} (\varphi_4 \circ f_3)(x) &= (g_3 \circ \varphi_3)(x) \\ &= g_3(0) \\ &= 0 \end{align}$$ なので, $\varphi_4$ が単射なことから $f_3(x) = 0$ です. つまり $x \in \ker f_3$ です.

行の完全性から $x = f_2(y)$ となる $y \in M_2$ が存在します. このとき $$\begin{align} (g_2 \circ \varphi_2)(y) &= (\varphi_3 \circ f_2)(y) \\ &= \varphi_3(x) \\ &= 0 \end{align}$$ なので $\varphi_2(y) \in \ker g_2$.

再び行の完全性から $g_1(z) = \varphi_2(y)$ となる $z \in N_1$ が存在します. そして $\varphi_1$ が全射なので $\varphi_1(w) = z$ となる $w \in M_1$ が存在します. すると $$\begin{align} \varphi_2(y) &= (g_1 \circ \varphi_1)(w) \\ &= (\varphi_2 \circ f_1)(w) \end{align}$$ で $\varphi_2$ が単射なので $y = f_1(w).$ よって $x = (f_2 \circ f_1)(w) = 0.$

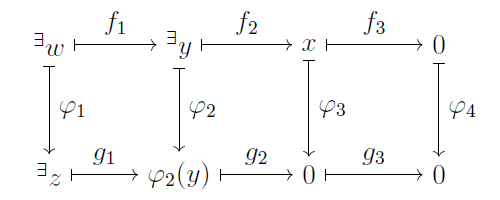
続いて 2. を証明します. $x \in N_3$ を任意に取ります. このとき $\varphi_4(y) = g_3(x)$ となる $y \in M_4$ があります. そして $$\begin{align} (\varphi_5 \circ f_4)(y) &= (g_4 \circ \varphi_4)(y) \\ &= (g_4 \circ g_3)(y) \\ &= 0 \end{align}$$ だから $\varphi_5$ の単射性から $f_4(y) = 0.$ つまり $y \in \ker f_4$ です.

行の完全性から $f_3(z) = y$ となる $z \in M_3$ が存在します.

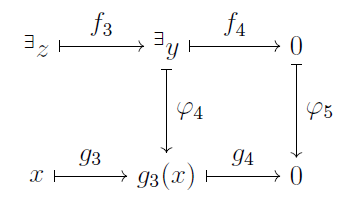
このとき $$\begin{align} g_3(x - \varphi_3(z)) &= g_3(x) - (g_3 \circ \varphi_3)(z) \\ &= \varphi_4(y) - (\varphi_4 \circ f_3)(z) \\ &= \varphi_4(y) - \varphi_4(y) \\ &= 0 \end{align}$$ なので, 再び行の完全性により $g_2(w) = x - \varphi_3(z)$ となる $w \in N_2$ が存在します. $\varphi_2$ の全射性により $\varphi_2(v) = w$ となる $v \in M_2$ が存在します.

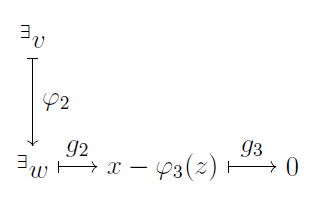
最後に $$\begin{align} \varphi_3(z + f_2(v)) &= \varphi_3(z) + (\varphi_3 \circ f_2)(v) \\ &= \varphi_3(z) + (g_2 \circ \varphi_2)(v) \\ &= \varphi_3(z) + g_2(w) \\ &= \varphi_3(z) + (x - \varphi_3(z)) \\ &= x \end{align}$$ となるので $\varphi_3$ は全射.

さあ, 飲み会だ!

さあ, これで皆さんも 5-lemma が証明できるようになりました. あとは飲み会で披露するだけです!

…って言っても, 数学科以外の飲み会でやるとドン引きされますね(多分).

…で, 終わりだと思った?

いくらなんでもこれで終わるのは Math Advent Calendar 2018 としては寂しいので, もうちょっと一般化しましょう.

完全圏

$ \DeclareMathOperator{\Ker}{\mathrm{Ker}} \DeclareMathOperator{\Cok}{\mathrm{Cok}} \DeclareMathOperator{\Img}{\mathrm{Im}} \DeclareMathOperator{\Coim}{\mathrm{Coim}} $

完全圏とは

ことを言います1.

命題1

完全列の可換図式2 $$\begin{CD} A @>>> B @>>> C @>>> D \\ @VV{a}V @VV{b}V @VV{c}V @VV{d}V \\ A' @>>> B' @>>> C' @>>> D' \\ @VVV \\ 0 \end{CD}$$ において $\Ker b \to \Ker c \to \Ker d$ は完全である.

(証明)

以下の二つの完全列の可換図式 $$\begin{CD} 0 @>>> E @>>> C @>>> D \\ @. @VV{e}V @VV{c}V @VV{d}V \\ 0 @>>> E' @>>> C' @>>> D' \end{CD}$$ と $$\begin{CD} A @>>> B @>>> E @>>> 0 \\ @VV{a}V @VV{b}V @VV{e}V @. \\ A' @>>> B' @>>> E' @>>> 0 \\ @VVV \\ 0 \end{CD}$$ に分けて考える. ここで $E = \Ker(C \to D) \cong \Cok(A \to B), E' = \Ker(C' \to D') \ \cong \Cok(A' \to B')$ であり, $e$ は核(および余核)の定義から自然に定まる, 上図を可換にする射である.

($\alpha$) $0 \to \Ker e \to \Ker c \to \Ker d$ は完全.
($\beta$) $\Ker b \to \Ker e$ は全射.

($\alpha$) については $\Ker e \to \Ker c$ が $\Ker c \to D$ の核であることから従う.

($\beta.1$) $\Cok b \to \Cok e$ は同型である(($\alpha$) の双対を使う).

($\beta.2$) 完全列の可換図式 $$\begin{CD} A' @>>> B' @>>> E' @>>> 0 \\ @VVV @VVV @VVV \\ 0 @>>> \Cok b @>>> \Cok e @>>> 0 \end{CD}$$ により $A' \to \Img b \to \Img e$ が完全であることがわかる. $A'$ を $B' \to E'$ の核で置き換えて ($\alpha$) を使う.

($\beta.3$) 以上から完全列の可換図式 $$\begin{CD} A @>>> B @>>> E @>>> 0 \\ @VV{a'}V @VV{b'}V @VV{e'}V @. \\ A' @>>> \Img b @>>> \Img e @>>> 0 \\ @VVV @VVV @VVV \\ 0 @. 0 @. 0 \end{CD}$$ を得る. $e'$ が $\Ker b' \to E$ の余核であることを確かめればよい.

命題2

完全列の可換図式 $$\begin{CD} @. @. @. 0 \\ @. @. @. @VVV \\ B @>>> C @>>> D @>>> E \\ @VV{b}V @VV{c}V @VV{d}V @VV{e}V \\ B' @>>> C' @>>> D' @>>> E' \end{CD}$$ において $\Cok b \to \Cok c \to \Cok d$ は完全である.

蛇の補題

命題3(蛇の補題)

完全列の可換図式 $$\begin{CD} @. @. @. @. 0 \\ @. @. @. @. @VVV \\ A @>>> B @>>> C @>>> D @>>> E \\ @VV{a}V @VV{b}V @VV{c}V @VV{d}V @VV{e}V \\ A' @>>> B' @>>> C' @>>> D' @>>> E' \\ @VVV \\ 0 \end{CD}$$ において次の列 $$\Ker b \to \Ker c \to \Ker d \stackrel{\partial}{\to} \Cok b \to \Cok c \to \Cok d$$ は完全である. より詳しく言うと

  1. $K = \Ker(C \to D')$ とおくと $K \to \Ker d$ が全射になる.
  2. $K' = \Cok(B \to C')$ とおくと $\Cok b \to K'$ が単射になる.
  3. 射の合成 $$K \to C \stackrel{c}{\to} C' \to K'$$ と射の合成 $$K \to \Ker d \stackrel{\partial}{\to} \Cok b \to K'$$ が等しくなるような射 $\partial \colon \Ker d \to \Cok b$ がただ一つ存在する.
  4. 上の6項からなる列が完全となる.
(証明)

$f$ を射 $C' \to \Ker(D' \to E')$ とする. 完全列の可換図式 $$\begin{CD} A @>>> B @>>> C @>>> D @>>> E \\ @VVV @VVV @VV{fc}V @VV{d}V @VV{e}V \\ 0 @>>> 0 @>>> \Img f @>>> D' @>>> E' \\ @VVV @VVV \\ 0 @. 0 \end{CD}$$ に命題1を2回使って $$B \to K \to \Ker d \to 0$$ が完全であることがわかる. 同様に $$0 \to \Cok b \to K' \to D'$$ が完全であることもわかる. これで (1), (2), (3) が示される.

命題1と命題2と双対性により $$\Ker c \to \Ker d \to \Cok b$$ が完全であることを示せばよい. そのためには $$\Ker c \to \Ker d \to K'$$ が完全であれば良い. 完全列の可換図式 $$\begin{CD} B @>>> K @>>> \Ker d @>>> 0 \\ @VV{id}V @VVV @VVV @VVV \\ B @>>> C' @>>> K' @>>> 0 \\ @VVV \\ 0 \end{CD}$$ と命題1から結論を得る.

完全圏での 5-lemma

完全圏における蛇の補題の系として, 直ちに 5-lemma が得られます.

終わりに

いかがだったでしょうか. 圏の世界になると要素が取れないので, 幾分証明がややこしいですが, 本質的には同じことを言っています. 5-lemma は(コ)ホモロジー論をやっていると必ずと言っていいほど出てくるので, 結論だけでも頭に入れておくと良いでしょう. ついでにさっと証明できるようになると格好良いかも?

参考文献

  1. 完全圏と Abel 圏の差は「有限積および有限余積が存在するかしないか」です. 完全圏では有限積および有限余積の存在は仮定されません.
  2. 「完全列の可換図式」とは縦, 横ともに完全系列になっているような可換図式のことです.

赤猫堂本舗「数学に関するよしなしごと」へ