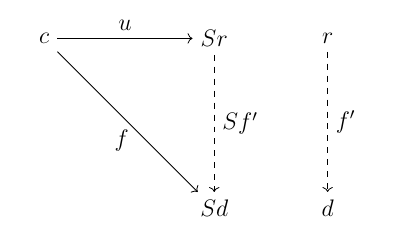
函手 $S \colon D \to C$ と対象 $c \in \mathcal{O}(C)$ があるとき, $c$ から $S$ への普遍射とは, $D$ の対象 $r$ と射 $u \colon c \to Sr$ の対 $\langle r, u\rangle$ で, $D$ の対象 $d$ と射 $f \colon c \to Sd$ の対 $\langle d, f\rangle$ の全てについて, $Sf' \circ u = f$ となる一意的な射 $f' \colon r \to d$ が存在するものである.

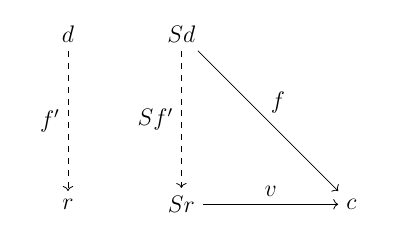
双対的に, $S$ から $c$ への普遍射も定義できる. これは $D$ の対象 $r$ と射 $v \colon Sr \to c$ の対 $\langle r, v\rangle$ で, $D$ の対象 $d$ と射 $f \colon Sd \to c$ の対 $\langle d, f\rangle$ の全てについて $f = v \circ Sf'$ となる射 $f' \colon d \to r$ が一意に存在するものである.
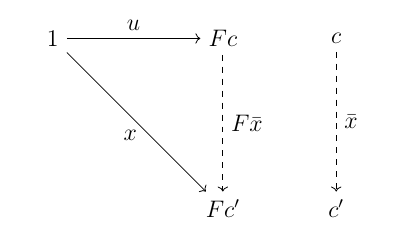
$C$ を局所小圏とする. $F \colon C \to \mathbf{Set}$ が表現可能であることは, 1 点集合 $1$ から $F$ への普遍射 $\langle c, u\rangle$ が存在することと同じである. 実際, 米田の補題により $F$ が上記のような普遍射を持てば, ($u \in Fc$ とみなして) $\tilde{u}(c') \colon C(c, c') \to Fc'$ は全単射だから $C(c, -) \cong F$ であり, 逆に自然同型 $\alpha \colon C(c, -) \cong F$ があれば $\hat{\alpha} \in Fc = \mathbf{Set}(1, Fc)$ とすれば $\langle c, \hat{\alpha}\rangle$ が $1$ から $F$ への普遍射である.
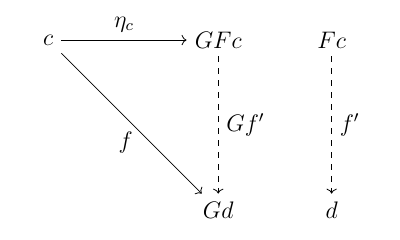
$G \colon D \to C$ が左随伴 $F \colon C \to D$ を持つならば, $f \in C(c, Gd)$ に対応する $f' \in D(Fc, d)$ があって, 次図が可換になる. 従って $c$ から $G$ への普遍射 $\langle Fc, \eta_c\rangle$ を持つ.
逆に, 各 $C(c, G(-))$ が普遍射 $\langle Fc, \eta_c\rangle$ を持てば, 下図から $F$ は函手となることがわかる.
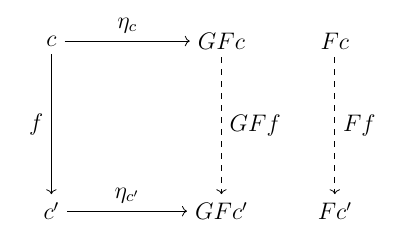
ここまでの議論により, (左)随伴の存在は
と同等であることがわかった.
$\mathbf{I}$ を小圏とする. 極限の定義自体にこの仮定は必要はないが, 大抵のケースは小圏で, しばしば有限である.
対角函手 $$\Delta \colon C \to C^\mathbf{I} = [\mathbf{I}, C]$$ を, 対象 $c$ に対して以下のような「定数函手」$\Delta c$ を対応させるものとする. $\Delta c$ は $\mathbf{I}$ の対象 $i$ に $c$ を, $\mathbf{I}$ の射に対して $1_c$ を対応させる. 射 $f \colon c \to c'$ に対しては, $i$ における値が $f$ に等しくなる自然変換 $\Delta f \colon \Delta c \stackrel{\bullet}{\to} \Delta c'$ を対応させる.
このとき, $C^\mathbf{I}$ の対象 $F \colon \mathbf{I} \to C$ に対して, $F$ から $\Delta$ への普遍射を余極限, $\Delta$ から $F$ への普遍射を極限という. 余極限は $\varinjlim F$, 極限は $\varprojlim F$ で表す.
全ての函手 $F \colon \mathbf{I} \to C$ に対して極限と余極限が存在すれば, 函手 $$\varinjlim, \varprojlim \colon C^\mathbf{I} \to C$$ が定義できるが, このとき $\varinjlim \dashv \Delta \dashv \varprojlim$ である.
一般に, 表現可能函手は極限を保存する. 式で書くと $S \colon \mathbf{I} \to C$ に対して $$C(c, \varprojlim S) \cong \varprojlim C(c, S) \quad \ (C(c, S) = Y^c \circ S \colon \mathbf{I} \to \mathbf{Set})$$ である.
これにより $G \colon D \to C$ が左随伴 $F \colon C \to D$ を持てば, $S \colon \mathbf{I} \to D$ に対して $$\begin{align} C(c, G(\varprojlim S)) &\cong D(Fc, \varprojlim S) \\ &\cong \varprojlim D(Fc, S) \\ &\cong \varprojlim C(c, GS) \\ &\cong C(c, \varprojlim GS) \end{align}$$ となるので, いわゆる「右随伴は極限を保つ」ことがわかる. 特に極限同士は交換する!
これの双対版は $$C(\varinjlim S, c) \cong \varprojlim C(S, c) \quad \ (C(S, c) = Y_c \circ S \colon \mathbf{I} \to \mathbf{Set})$$ である. $C^\mathrm{op}$ の極限は余極限だからである. 右辺が余極限ではないことに注意. このことから双対的に「左随伴は余極限を保つ」ことがわかる(故に余極限同士も交換する).
余極限の定義において $\mathbf{I} = \mathbf{0}$ (空圏)としてみたらどうなるだろう. このとき $\Delta \colon C \to C^\mathbf{0} \cong \mathbf{1}$ である. ただ一つの函手 $O \colon \mathbf{0} \to C$ に対して, $O$ から $\Delta$ への普遍射があることは, ある対象 $i$ が存在して, 任意の $c$ に対して射 $i \to c$ が存在すると言っていることになる. すなわち始対象である. 同様に終対象は極限である.
積やファイバー積(引き戻し), イコライザは極限の特別な例として多くの参考書籍に出てくる. 我々はモノ射の定義をしたが, $f \colon c \to c'$ がモノであることは可換図式 $$\begin{CD} c @>{1}>> c \\ @V{1}VV @VV{f}V \\ c @>>{f}> c' \end{CD}$$ が引き戻しの図式であることと同値である. つまり右随伴(例えば忘却函手!)はモノ射を保つ.