休憩 : モノイダル圏と豊穣圏

モノイダル圏

双圏の言葉を使うと, モノイダル圏を一行で定義できる.

定義

ただ一つの対象を持つ双圏をモノイダル圏と言う.

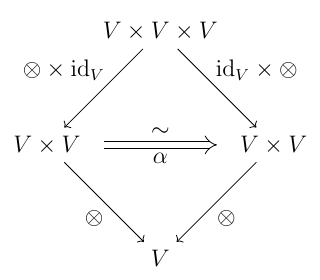
ただ一つの対象を持つ圏はモノイドと同一視できるが, それの双圏版である. モノイダル圏 $\mathcal{B}$ のただ一つの対象 $*$ に対する $\mathcal{B}(*, *)$ を $V$ と置く. このとき二項演算 $\otimes := C_{***} \colon V \times V \to V$ と「単位元」 $I := \mathrm{id}_* \in V$ がある. そして以下のような自然同型がある.

• $\lambda \colon I \otimes - \Rightarrow \mathrm{id}_V$
• $\rho \colon - \otimes I \Rightarrow \mathrm{id}_V$

コヒーレンス条件を書き下すと以下のようになる.

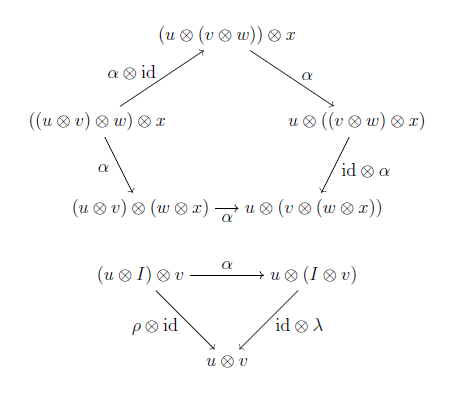
つまりモノイダル圏とはこのような条件を満たす組 $\langle V, \otimes, I, \alpha, \lambda, \rho \rangle$ のことだと思って差し支えない.

豊穣圏

$\langle V, \otimes, I, \alpha, \lambda, \rho \rangle$ をモノイダル圏とするとき, $\mathcal{C}$ が $V$-豊穣圏であるとは

• $\mathcal{C}$ の対象の集まり
• $a, b \in \mathcal{C}$ に対して $V$ の対象 $\mathcal{C}(a, b)$
• $a, b, c \in \mathcal{C}$ に対して $V$ の射 $m_{abc} \colon \mathcal{C}(b, c) \otimes \mathcal{C}(a, b) \to \mathcal{C}(a, b)$
• $a \in \mathcal{C}$ に対して $V$ の射 $j_a \colon I \to \mathcal{C}(a, a)$

• 以下の可換図式

  

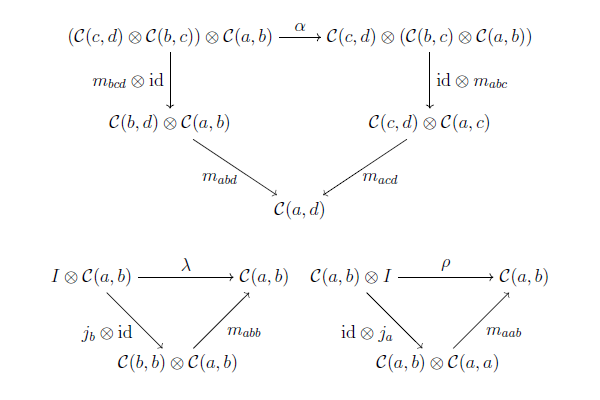
が与えられるものである. この定義を使うと, 局所小圏は $\mathbf{Set}$-豊穣圏であり, 2-圏は $\mathbf{Cat}$(ないし $\mathbf{CAT}$)-豊穣圏と考えることができる.

注意 : 定義をよく読むとわかると思うが, 豊穣圏においては対象間の射は一般には取れない.

戻る