双圏へのアイデア

2-圏とは何だったのか

そもそも2-圏 $\mathcal{B}$ とは

• 対象 $a, b, \dots$
• (1-)射 $f, g, \dots$
• 変換(= 2-射) $\alpha, \beta, \dots$

があって, $a$ から $b$ への射の全体を $\mathcal{B}(a, b)$ とするとき, これが(2-圏の垂直構造について)圏になっている. 水平構造についての恒等射 $1_a$ は $\mathcal{B}(a, a)$ の対象である. これを函手 $I_a \colon \mathbf{1} \to \mathcal{B}(a, a)$ とみなす.

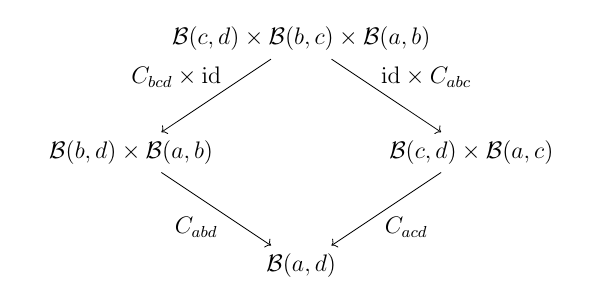
さらに次図が可換である. ここで $$C_{abc} \colon \mathcal{B}(b, c) \times \mathcal{B}(a, b) \ni (\beta, \alpha) \mapsto \ \beta \star \alpha \in \mathcal{B}(a, c)$$ である. そもそも $C_{abc}$ が函手であることは $$\begin{align} s_\circ C_{abc}(\beta, \alpha) &= s_\circ(\beta \star \alpha) \\ &= s_\circ \beta \star s_\circ \alpha \\ &= C_{abc}(s_\circ \beta, s_\circ \alpha) \\ &= C_{abc} s_\circ(\beta, \alpha) \end{align}$$ や, (同様に) $t_\circ C_{abc} = C_{abc} t_\circ$ であること, そして $$\begin{align} C_{abc}((\beta', \alpha') \circ (\beta, \alpha)) &= C_{abc}(\beta' \circ \beta, \alpha' \circ \alpha) \\ &= (\beta' \circ \beta) \star (\alpha' \circ \alpha) \\ &= (\beta' \star \alpha') \circ (\beta \star \alpha) \\ &= C_{abc}(\beta', \alpha') \circ C_{abc}(\beta, \alpha) \end{align}$$ からわかる.

「等しい」から「同型」へ

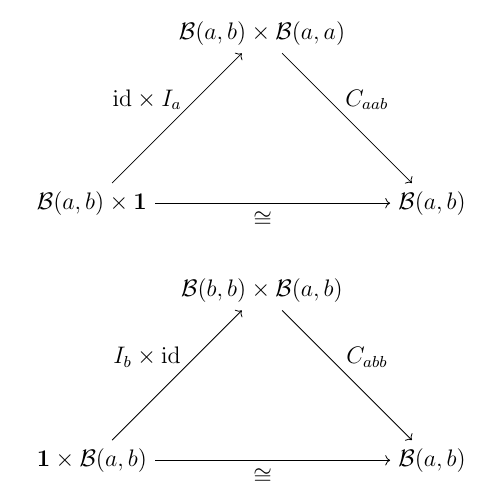
上記の可換図式は, 各々, 二通りの函手の合成が等しいと言っているのであるが, 「函手が等しい」というのは実は圏論ではかなりきつい条件である. そこで, これらを全て「(自然)同型」で置き換えたらどうなるだろうか, という発想から出てきたのが双圏(bicategory)である.

戻る