双圏であるが2-圏ではない例を三つほど挙げよう. 一つ目は
である. 良く知られたように, $(S, R)$-両側加群 $A$ に対して $$S \otimes_S A \cong A, A \otimes_R R \cong A$$ であり, さらに $(T, S)$-両側加群 $B$ と $(U, T)$-両側加群 $C$ があれば自然な同型 $$(C \otimes_T B) \otimes_S A \cong C \otimes_T (B \otimes_S A)$$ が成り立つから, これは双圏の例になっている.
もう一つの例は fundamental 2-groupoid と呼ばれるものである.
$a \stackrel{f}{\to} b \stackrel{g}{\to} c \stackrel{h}{\to} d$ のとき, $\alpha_{hgf} \colon [0, 1] \times [0, 1] \to X$ を $$\alpha_{hgf}(s, t) = \begin{cases} f\left(\frac{4t}{2 - s}\right) & \left(0 \leq t \leq \frac{2 - s}{4}\right) \\ g(4t - 2 + s) & \left(\frac{2 - s}{4} \leq t \leq \frac{3 - s}{4}\right) \\ h\left(\frac{4t - 3 + s}{1 + s}\right) & \left(\frac{3 - s}{4} \leq t \leq 1\right) \end{cases}$$ とすれば $\alpha_{hgf} \colon (h \star g) \star f \Rightarrow h \star (g \star f)$.
また, $a \stackrel{f}{\to} b$ に対して $\lambda_f \colon [0, 1] \times [0, 1] \to X$ と $\rho_f \colon [0, 1] \times [0, 1] \to X$ を $$\lambda_f(s, t) = \begin{cases} f\left(\frac{2t}{1 + s}\right) & \left(0 \leq t \leq \frac{1 + s}{2}\right) \\ b & \left(\frac{1 + s}{2} \leq t \leq 1\right), \end{cases}$$ $$\rho_f(s, t) = \begin{cases} a & \left(0 \leq t \leq \frac{1 - s}{2}\right) \\ f\left(\frac{2t - 1 + s}{1 + s}\right) & \left(\frac{1 - s}{2} \leq t \leq 1\right) \end{cases}$$ とすれば, $\lambda_f \colon i_b \star f \Rightarrow f, \rho_f \colon f \star i_a \Rightarrow f$. この双圏は $\Pi_2(X)$ と表記される.
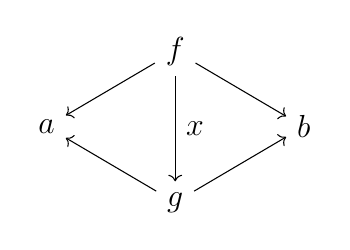
他にも, pullback を持つ圏 $C$ の「スパン」と呼ばれるものの全体 $\mathrm{Span}(C)$ がある. 対象(0-射)は基礎圏 $C$ の対象, 1-射は「スパン」 $a \leftarrow f \rightarrow b$, $\mathrm{Span}(C)(a, b)$ はスパンを対象に持ち, 対象 $f, g$ 間の射として次図を可換にする $C$ の射を取ることによって得られる圏とする.

1-射の合成は(カノニカルな) pullback を用いて下図で定義される.
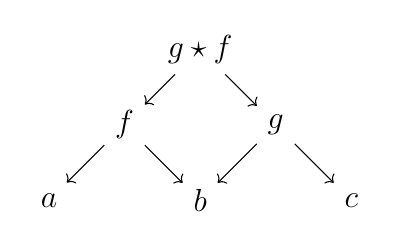
$\mathrm{Span}(C)(a, a)$ の単位射は $a \stackrel{\mathrm{id}_a}{\leftarrow} a \stackrel{\mathrm{id}_a}{\rightarrow} a$ である. これが実際に双圏になっていることは pullback の普遍性を用いて比較的容易に示せるので, 各自確かめられたし.