次図の自然同型がある.
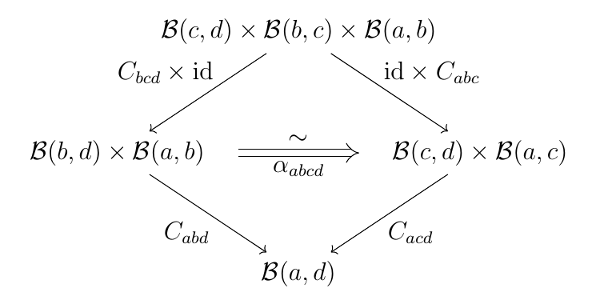
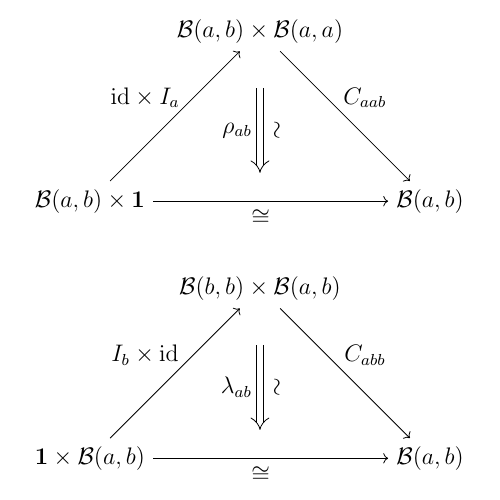
次図の自然変換の等式が成り立つ(コヒーレンス条件). ただしスペースの都合上 $$\mathcal{B}abc := \mathcal{B}(b, c) \times \mathcal{B}(a, b), \ \mathcal{B}abcd := \mathcal{B}(c, d) \times \mathcal{B}(b, c) \times \mathcal{B}(a, b)$$ のように略記している.
$\mathcal{B}$ が双圏(bicategory)であるとは以下の全てを満たすことである.
次図の自然同型がある.


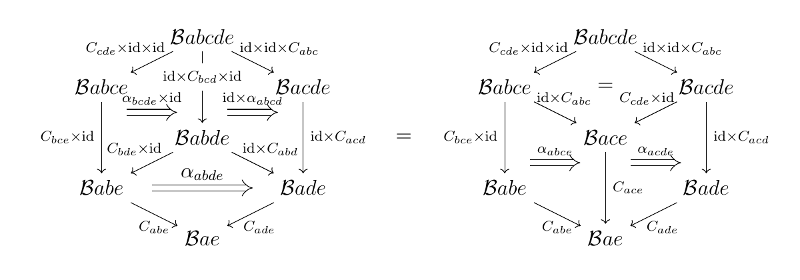
次図の自然変換の等式が成り立つ(コヒーレンス条件). ただしスペースの都合上 $$\mathcal{B}abc := \mathcal{B}(b, c) \times \mathcal{B}(a, b), \ \mathcal{B}abcd := \mathcal{B}(c, d) \times \mathcal{B}(b, c) \times \mathcal{B}(a, b)$$ のように略記している.


上記の $\alpha_{abcd}, \rho_{ab}, \lambda_{ab}$ が全ての $a, b, c, d$ について恒等変換であるとき, $\mathcal{B}$ は2-圏であると言う(再定義).
コヒーレンス条件の図式は何を言いたいのだろうか. 例えば合成に関して言えば, 四つの射の合成について, 自然同型 $$((k \star h) \star g) \star f \cong k \star (h \star (g \star f))$$ を与える方法が $$((k \star h) \star g) \star f \stackrel{\alpha \star f}{\cong} (k \star (h \star g)) \star f \ \stackrel{\alpha}{\cong} k \star ((h \star g) \star f) \ \stackrel{k \star \alpha}{\cong} k \star (h \star (g \star f))$$ と $$((k \star h) \star g) \star f \stackrel{\alpha}{\cong} (k \star h) \star (g \star f) \ \stackrel{\alpha}{\cong} k \star (h \star (g \star f))$$ の見かけ上二通りあるが, 両者が等しいことを言っている(五角図式).
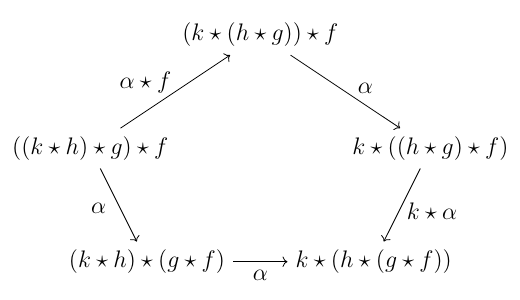
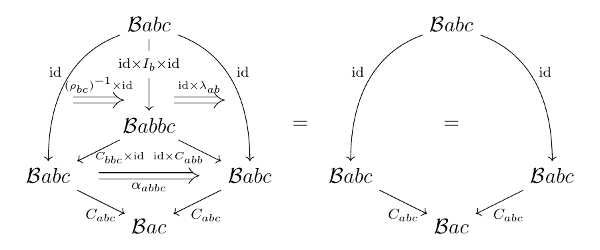
恒等射についても同様の可換図式がある.
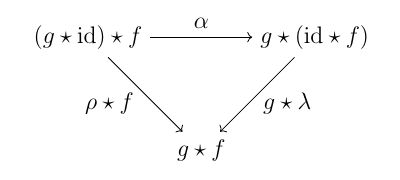
ここで気になるのが, 「五つ以上の射の合成に関してはもっと複数の自然同型の与え方があるのでは?」といったことであるが, 実は上記の二つの条件さえ認めてしまえば問題がない(コヒーレンス定理). これを証明するために, 後で双圏版の米田の補題を証明する.
後に使う補題をいくつか証明しておく.
$a \stackrel{f}{\to} b \stackrel{g}{\to} c$ のとき, 圏 $\mathcal{B}(a, c)$ における次図は可換.
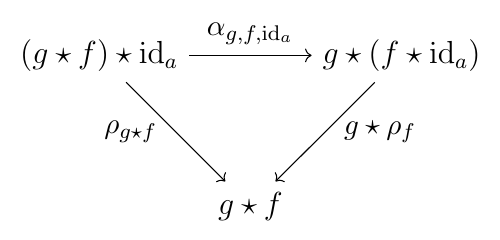
下図の三角柱において, 側面は $\rho$ が自然同型だから全て可換である. 示したいのは底面の三角形の可換性だから, そのためには上面の三角形の可換性を示せばよい.
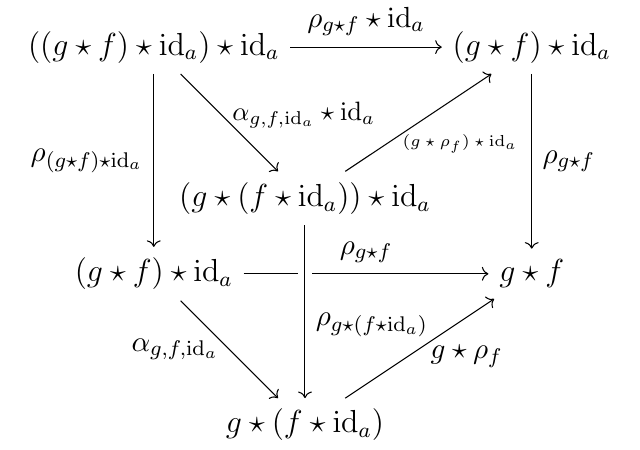
そのために以下の図式を考える. $(**)$ の可換性が示したい部分である.
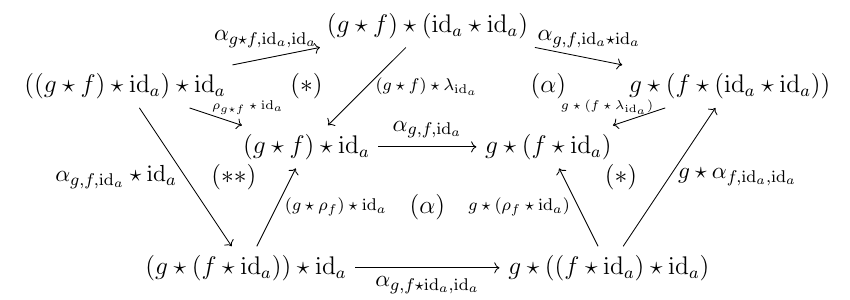
上の図式において, $(\alpha)$ の部分は $\alpha$ が自然同型だから可換, $(*)$ の部分と一番外側の五角形は bicategory の coherence 条件から可換である. 従って, 示したかった $(**)$ の部分も可換である. (証明終)
$a \stackrel{f}{\to} b \stackrel{g}{\to} c$ のとき, 圏 $\mathcal{B}(a, c)$ における次図は可換.
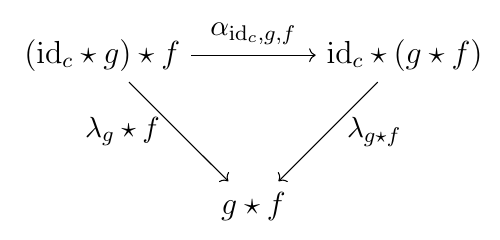
証明は補題1とほぼ同様なので省略する.
$\lambda_{\mathrm{id}_a} = \rho_{\mathrm{id}_a} \colon \mathrm{id}_a \star \mathrm{id}_a \Rightarrow \mathrm{id}_a$ である.
補題1などと同様に $\mathrm{id}_a \star \lambda_{\mathrm{id}_a} = \mathrm{id}_a \star \rho_{\mathrm{id}_a}$ を示せばよい.
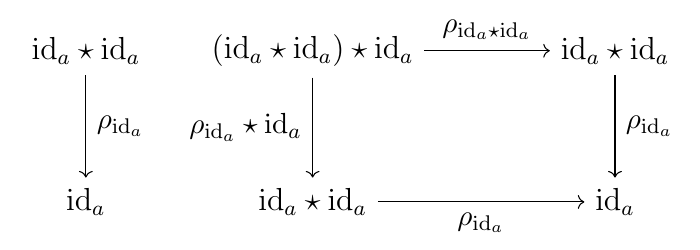
$\rho$ の自然性から上図は可換であるが, $\rho$ は自然同型なので $\rho_{\mathrm{id}_a} \star \mathrm{id}_a = \rho_{\mathrm{id}_a \star \mathrm{id}_a}$ がわかる.
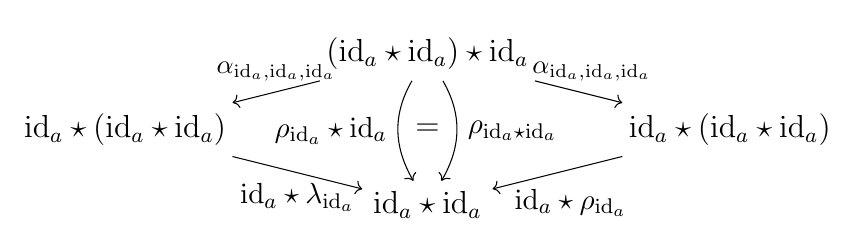
上図において, 左側は bicategory の coherence 条件から可換, 右側は補題1から可換. $\alpha$ が自然同型のため結論を得る. (証明終)