$\newcommand{\mapsfrom}{\leftarrow\!\shortmid}$ $F \colon C \to D, G \colon D \to C$ を函手とする. $F$ が $G$ の左随伴である, または $G$ が $F$ の右随伴である($F \dashv G$ と表す)とは, 同型 $$D(F(c), d) \cong C(c, G(d))$$ が各 $c \in \mathcal{O}(C), d \in \mathcal{O}(D)$ において「自然に」成り立つことをいう.
ここで「自然に」というのは $$(F(c) \stackrel{g}{\to} d) \mapsto (c \stackrel{\bar{g}}{\to} G(d)),$$ $$(F(c) \stackrel{\bar{f}}{\to} d) \mapsfrom (c \stackrel{f}{\to} G(d))$$ なる「転置」(2 回施すと元に戻る)があり, $p \colon c' \to c, q \colon d \to d'$ に対して $$\overline{(q \circ g)} = G(q) \circ \bar{g}, \overline{(f \circ p)} = \bar{f} \circ F(p)$$ が成り立つことを言う. これは $C, D$ が局所小圏と仮定すれば双函手の自然同型 $$D(F(-), -) \cong C(-, G(-)) \colon C^\mathrm{op} \times D \to \mathbf{Set}$$ と同じである.
明らかに左随伴と右随伴は互いに他の双対概念である.
$k$-係数ベクトル空間 $V$ を単に集合と思うことは函手 $U \colon \mathbf{Vect}_k \to \mathbf{Set}$ を導く. 一方, 集合 $S$ に対し, $S$ を基底に持つベクトル空間を対応させることは別の函手 $F \colon \mathbf{Set} \to \mathbf{Vect}_k$ を導く. このとき $$\mathbf{Vect}_k(F(S), V) \cong \mathbf{Set}(S, U(V))$$ は $S, V$ について自然である. 故に $F \dashv U$.
もう一つの例を挙げる. Abel 群 $A$ を通常の群とみなす函手 $U \colon \mathbf{Ab} \to \mathbf{Grp}$ がある. 一方で, 群 $G$ の Abel 化 $G \mapsto G/[G, G]$ は函手 $F \colon \mathbf{Grp} \to \mathbf{Ab}$ を導く. このとき $$\mathbf{Ab}(F(G), A) \cong \mathbf{Grp}(G, U(A))$$ も $G, A$ について自然であるから $F \dashv U$.
このように, ある構造を持つ集合を, その構造を忘れてより単純な対象とみなす「忘却函手」は多くの場合左随伴を持つ.
最後に, 忘却函手が左随伴と右随伴を持つ例を証明なしに上げておこう. 忘却函手 $U \colon \mathbf{Top} \to \mathbf{Set}$ について, 集合に離散位相を導入する函手 $D \colon \mathbf{Set} \to \mathbf{Top}$ と密着位相を導入する函手 $I \colon \mathbf{Set} \to \mathbf{Top}$ について, $D \dashv U \dashv I$.
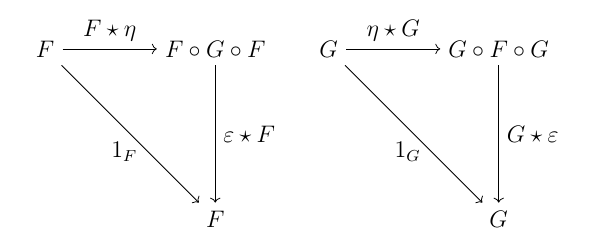
$F \dashv G$ のとき, 自然性 $$\overline{(q \circ g)} = G(q) \circ \bar{g}, \overline{(f \circ p)} = \bar{f} \circ F(p)$$ において $g = q = 1_{F(c)}, f = p = 1_{G(d)}$ と置くことで $$(c \stackrel{\eta_c}{\to} (G \circ F)(c)) \ = \overline{\left(F(c) \stackrel{1}{\to} F(c)\right)},$$ $$((F \circ G)(d) \stackrel{\varepsilon_d}{\to} d) \ = \overline{\left(G(d) \stackrel{1}{\to} G(d)\right)}$$ が得られ, これらは単位, 余単位と呼ばれる自然変換 $$\eta \colon 1_C \to G \circ F, \varepsilon \colon F \circ G \to 1_D$$ を定める. このとき, 自然変換に関して以下の三角等式が成り立つ(水平合成において恒等自然変換を函手自身と同一視している). $$(\varepsilon \star F) \circ (F \star \eta) = 1_F, \ (G \star \varepsilon) \circ (\eta \star G) = 1_G$$

上図はそれぞれ函手圏 $[C, D], [D, C]$ における可換図式である. 逆に, 三角等式を満たすような自然変換の組 $$\eta \colon 1_C \to G \circ F, \varepsilon \colon F \circ G \to 1_D$$ は随伴 $F \dashv G$ を定める(証明略).